RACIOCÍNIO LÓGICO MATEMÁTICO

Sugestão de Livro
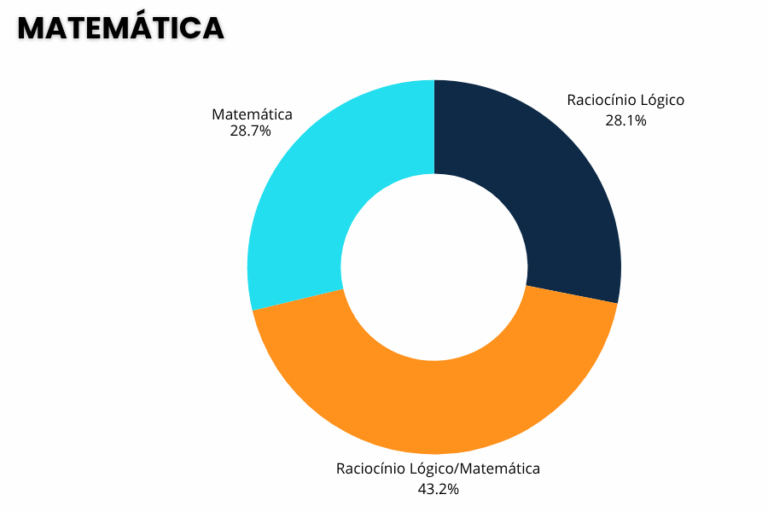
Raciocínio Lógico - 28,11%
O raciocínio lógico é uma das áreas mais cobradas em concursos, pois avalia a capacidade de analisar, deduzir e interpretar informações. Ele se baseia em proposições, operações lógicas e relações entre conjuntos, servindo para resolver problemas de forma estruturada.
1. Tabelas-Verdade e Proposições
Uma proposição é uma sentença que pode ser verdadeira (V) ou falsa (F).
- Proposição simples: não contém conectivos (ex.: “A Terra é redonda”).
- Proposição composta: formada por conectivos lógicos.
Principais operadores lógicos:
- Negação (¬ ou ~): inverte o valor lógico.
- Conjunção (∧): só é verdadeira se ambas forem verdadeiras.
- Disjunção (∨): é verdadeira se ao menos uma for verdadeira.
- Condicional (→): só é falsa se a primeira for verdadeira e a segunda falsa.
- Bicondicional (↔): verdadeira quando as proposições têm o mesmo valor.
As tabelas-verdade mostram todos os possíveis resultados para proposições compostas, sendo uma ferramenta básica para análise.
2. Negação e Leis de De Morgan
A negação de uma proposição composta segue as Leis de De Morgan:
- Negação de uma conjunção: ¬(p ∧ q) ≡ (¬p ∨ ¬q)
("não [p e q]" equivale a "[não p] ou [não q]"). - Negação de uma disjunção: ¬(p ∨ q) ≡ (¬p ∧ ¬q).
Essas equivalências aparecem com frequência em questões.
3. Equivalências Lógicas
Duas proposições são logicamente equivalentes quando possuem os mesmos valores lógicos em todas as situações.
Exemplo clássico:
- Condicional (p → q) é equivalente a (¬p ∨ q).
- A contrarrecíproca (¬q → ¬p) também é equivalente a (p → q).
4. Lógica de Argumentação e Diagramas
Um argumento válido é aquele em que, se as premissas forem verdadeiras, a conclusão também será.
É comum o uso de:
- Diagramas lógicos (setas e estruturas) para visualizar relações.
- Operadores lógicos para formalizar raciocínios.
5. Tautologia, Contradição e Contingência
- Tautologia: proposição sempre verdadeira.
- Contradição: proposição sempre falsa.
- Contingência: pode ser verdadeira ou falsa, dependendo do caso.
6. Proposições Categóricas e Verdades/Mentiras
As proposições categóricas relacionam classes e conjuntos (“Todo A é B”, “Nenhum A é B”). São úteis em problemas com pessoas que sempre mentem ou dizem a verdade, típicos em provas.
7. Diagramas de Venn (Conjuntos)
Usados para representar graficamente relações de inclusão, interseção e união entre conjuntos. Facilitam a resolução de problemas envolvendo grupos e categorias.
EDITAL VERTICALIZADO DINÂMICO
Marque abaixo todos os tópicos que você já domina da matéria. Assim, você terá um controle mais preciso do que já está consolidado nos editais verticalizados dinâmicos do curso.
| RACIOCÍNIO LÓGICO | ||||||||||||||||||||||||||||
| Fundamentos de Lógica | ||||||||||||||||||||||||||||
| Tabelas-Verdade | ||||||||||||||||||||||||||||
| Proposições Simples e Compostas e Operadores Lógicos | ||||||||||||||||||||||||||||
| Equivalência Lógica e Negação de Proposições | ||||||||||||||||||||||||||||
| Negação - Leis de Morgan (Negativa de uma Proposição Composta) | ||||||||||||||||||||||||||||
| Equivalências - Proposições Logicamente Equivalentes | ||||||||||||||||||||||||||||
| Lógica de Argumentação - Diagramas e Operadores Lógicos | ||||||||||||||||||||||||||||
| Tautologia, Contradição e Contingência | ||||||||||||||||||||||||||||
| Proposições Categóricas | ||||||||||||||||||||||||||||
| Verdades e Mentiras | ||||||||||||||||||||||||||||
| Diagramas de Venn (Conjuntos) | ||||||||||||||||||||||||||||
Links de Questões do site QConcursos dos Assuntos Acima
- Questões Muito Fáceis -
- Questões Fáceis -
- Questões Medianas -
- Questões Difíceis -
- Questões Muito Difíceis -
Raciocínio Lógico com Matemática - 43,16%
Essa parte mistura raciocínio lógico e cálculos matemáticos, exigindo que o candidato saiba interpretar informações, organizar dados e aplicar fórmulas básicas. É muito cobrada em provas, especialmente quando envolve contagem, chances e deduções lógicas.
1. Análise Combinatória (RL e Matemática)
A análise combinatória ajuda a contar possibilidades sem listar todas elas. Os principais conceitos cobrados são:
- Princípio Fundamental da Contagem (PFC): quando um evento pode ocorrer de "m" maneiras e outro de "n" maneiras, juntos eles podem ocorrer de "m vezes n" formas.
- Permutação: é a organização de todos os elementos de um grupo, levando em conta a ordem. Fórmula: "P de n é igual a n fatorial" (n vezes n-1, vezes n-2 e assim por diante até 1).
- Combinação: é a escolha de elementos, sem importar a ordem. Fórmula: "C de n, k é igual a n fatorial dividido por k fatorial vezes (n menos k) fatorial".
- Arranjo: é a escolha de elementos em que a ordem importa. Fórmula: "A de n, k é igual a n fatorial dividido por (n menos k) fatorial".
Esses conceitos aparecem em problemas como formação de senhas, distribuição de pessoas e organização de grupos.
2. Probabilidade (RL e Matemática)
A probabilidade mede a chance de um evento ocorrer.
Fórmula básica:
"Probabilidade de um evento é igual ao número de casos favoráveis dividido pelo número de casos possíveis".
Exemplos de aplicação:
- Probabilidade de tirar uma carta específica em um baralho.
- Chances de um número sair no dado.
- Probabilidades condicionais (quando um evento depende de outro).
Esses cálculos aparecem tanto em problemas matemáticos diretos quanto em questões lógicas que envolvem contagem.
3. Problemas Lógicos e Matemáticos
São questões que exigem interpretação e organização de dados. Os formatos mais comuns são:
- Problemas com tabelas e pistas, para descobrir relações (como quem mora em qual casa).
- Questões que exigem regra de três, porcentagem ou proporções.
- Situações que pedem sistemas de equações simples para chegar ao resultado.
4. Sequências Lógicas
As sequências podem envolver números, letras, palavras ou figuras. É necessário identificar padrões como:
- Progressões aritméticas ou geométricas.
- Alternâncias (pares, ímpares, crescentes ou decrescentes).
- Regras ocultas (somar, multiplicar, inverter, ou padrões visuais).
5. Análise de Tabelas e Gráficos
As bancas costumam apresentar gráficos de colunas, setores (pizza), linhas e tabelas. O candidato precisa:
- Interpretar valores absolutos e percentuais.
- Comparar variações e identificar tendências.
- Realizar cálculos simples como somas, médias e porcentagens.
Essas questões muitas vezes exigem mais interpretação do que cálculos complexos.
EDITAL VERTICALIZADO DINÂMICO
Marque abaixo todos os tópicos que você já domina da matéria. Assim, você terá um controle mais preciso do que já está consolidado nos editais verticalizados dinâmicos do curso.
| RACIOCÍNIO LÓGICO/MATEMÁTICA | ||||||||||||||||||||||||||||
| Análise Combinatória em Raciocínio Lógico | ||||||||||||||||||||||||||||
| Análise Combinatória em Matemática | ||||||||||||||||||||||||||||
| Probabilidade (em Raciocínio Lógico) | ||||||||||||||||||||||||||||
| Probabilidade (em Matemática) | ||||||||||||||||||||||||||||
| Problemas Lógicos | ||||||||||||||||||||||||||||
| Problema (em Matemática) | ||||||||||||||||||||||||||||
| Raciocínio Matemático (em Raciocínio Lógico) | ||||||||||||||||||||||||||||
| Raciocínio Lógico (em Matemática) | ||||||||||||||||||||||||||||
| Sequências Lógicas de Números, Letras, Palavras e Figuras | ||||||||||||||||||||||||||||
| Análise de Tabelas e Gráficos | ||||||||||||||||||||||||||||
Links de Questões do site QConcursos dos Assuntos Acima
- Questões Muito Fáceis -
- Questões Fáceis -
- Questões Medianas -
- Questões Difíceis -
- Questões Muito Difíceis -
Matemática - 28,73%
Em provas, a matemática básica aparece em situações práticas, exigindo rapidez em cálculos e domínio de conceitos fundamentais. Os principais tópicos envolvem números, medidas, proporções e problemas aplicados.
1. Sistemas de Numeração e Operações Fundamentais
O sistema de numeração usado é o decimal, baseado em dez dígitos (0 a 9) e posições com potências de dez (unidade, dezena, centena...).
Operações básicas cobradas:
- Adição e subtração.
- Multiplicação e divisão.
- Potenciação e radiciação (usadas em questões com crescimento ou áreas).
Muitas bancas cobram operações com números grandes ou com casas decimais, exigindo atenção aos alinhamentos.
2. Frações e Números Decimais
- Frações próprias: numerador menor que o denominador.
- Frações impróprias: numerador maior ou igual ao denominador.
- Frações equivalentes: representam o mesmo valor.
Conversões importantes:
- Para decimal, basta dividir o numerador pelo denominador.
- Para porcentagem, multiplica-se o valor decimal por 100.
Operações básicas (soma, subtração, multiplicação e divisão) também caem com frequência.
3. Razão, Proporção e Números Proporcionais
- Razão: comparação entre dois valores por divisão.
Exemplo: a razão de 8 para 4 é 8 dividido por 4, que resulta em 2. - Proporção: igualdade entre duas razões.
Exemplo: 2 dividido por 4 é igual a 5 dividido por 10.
Os números proporcionais aparecem em problemas que envolvem aumento, redução ou comparação de grandezas (como velocidade, tempo, quantidade de pessoas).
4. Sistema de Unidades de Medidas
O Sistema Internacional (SI) é o mais utilizado:
- Comprimento: milímetro, centímetro, metro e quilômetro.
- Massa: grama, quilograma e tonelada.
- Capacidade: mililitro e litro.
- Área e volume: metro quadrado e cúbico.
Conversões são comuns em prova:
- Para cada passo entre unidades, multiplica-se ou divide-se por 10, 100 ou 1000, dependendo da escala.
5. Regra de Três
Permite resolver problemas de proporção:
- Simples: relaciona duas grandezas.
- Composta: relaciona três ou mais grandezas.
O método consiste em montar uma proporção e resolver multiplicando em cruz.
6. Porcentagem
Muito cobrada em concursos.
Cálculo básico:
"Porcentagem de um valor é igual a (valor vezes a porcentagem) dividido por 100".
Exemplo: 20% de 150 é igual a 150 vezes 20 dividido por 100, que resulta em 30.
7. Áreas e Perímetros
Fórmulas mais usadas:
- Quadrado: área = lado vezes lado; perímetro = quatro vezes o lado.
- Retângulo: área = base vezes altura; perímetro = duas vezes (base mais altura).
- Triângulo: área = (base vezes altura) dividido por 2.
- Círculo: área = pi vezes raio ao quadrado; perímetro (circunferência) = 2 vezes pi vezes raio.
Esses cálculos aparecem em problemas diretos ou contextualizados (como terrenos, pisos e construções).
EDITAL VERTICALIZADO DINÂMICO
Marque abaixo todos os tópicos que você já domina da matéria. Assim, você terá um controle mais preciso do que já está consolidado nos editais verticalizados dinâmicos do curso.
| MATEMÁTICA | ||||||||||||||||||||||||||||
| Sistemas de Numeração e Operações Fundamentais | ||||||||||||||||||||||||||||
| Frações e Números Decimais | ||||||||||||||||||||||||||||
| Razão e Proporção; e Números Proporcionais | ||||||||||||||||||||||||||||
| Sistema de Unidade de Medidas | ||||||||||||||||||||||||||||
| Regra de Três | ||||||||||||||||||||||||||||
| Porcentagem | ||||||||||||||||||||||||||||
| Áreas e Perímetros | ||||||||||||||||||||||||||||
Links de Questões do site QConcursos dos Assuntos Acima
- Questões Muito Fáceis -
- Questões Fáceis -
- Questões Medianas -
- Questões Difíceis -
- Questões Muito Difíceis -


